Binary search algorithm and usage
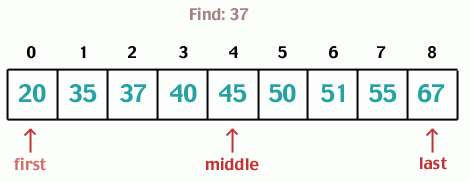
A binary search algorithm finds the position of a specified value within a sorted array. In each step, the algorithm compares the input key value with the key value of the middle element of the array. If the keys match, then a matching element has been found then its position, is returned. If the key is less than the middle element, then the algorithm repeats on the sub-array to the left of the middle element or, if the input key is greater, on the sub-array to the right. If the remaining array to be searched is reduced to zero, then the key cannot be found in the array and a special “Not found” indication is returned.
The binary search algorithm is the fastest algorithm to find the element in sorted array.
- Worst case performance: O(log2n)
- Best case performance: O(1)
Practical examples of binary search algorithm:
- Implementing a “switch() … case:” construct in a virtual machine where the case labels are individual integers. If there are 100 cases, the correct entry can be find in 6 to 7 steps using binary search, where as sequence of conditional branches takes on average 50 comparisons.
- Doing fast substring lookup using suffix arrays, which contain all the suffixes of the set of searchable strings in lexiographic ordering.
- Binary search algorithm is used in 3D games and applications. Space is divided into a tree structure and a binary search is used to retrieve which subdivisions to display according to a 3D position and camera.
Steps to implement binary search algorithm:
- Compare searchElement with the middle element of array.
- If searchElement matches with middle element, we return the mid index.
- Else If searchElement is greater than the mid element, then searchElement can only lie in right half subarray after the mid element. So we recur for right half.
- Else (searchElement is smaller) recur for the left half.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
package com.learningsolo.datastructures; public class BinarySearchImpl { public static void main(String[] args) { int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }; int searchElement = 8; if (isElementPresent(arr, searchElement)) { System.out.println("Search Element " + searchElement + " found."); } else { System.out.println("Search Element " + searchElement + " not found."); } } // isElementPresent implements binary search algorithm to search element in // array public static boolean isElementPresent(int arr[], int searchElement) { int first = 0; int last = arr.length - 1; int mid = (first + last) / 2; while (first <= last) { if (arr[mid] > searchElement) { last = mid - 1; } if (arr[mid] < searchElement) { first = mid + 1; } if (arr[mid] == searchElement) { return true; } mid = (first + last) / 2; } return false; } } |